3849. Tree
A weighted tree
is a tree where each edge is labeled with a number representing the edge’s
length. All lengths are positive. For each node, you have to find the maximum
possible distance to any other node in the tree.
Input. Contains
the description of the tree. The first line contains the number of vertices n (2 ≤ n
≤ 50000) in a tree. Each
of the following n – 1 lines contains the
description of the tree's edges. Each edge is described by three positive
integers. The first two integers are the labels of the nodes connected by this
edge, ranging from 1 to n,
the third number – the length of the edge. The total length of all edges does
not exceed 231 – 1. It is guaranteed that the description of
the tree is correct.
Output. Print
exactly n lines: the k-th line contains the distance from
node k (k = 1..n) to the most
distant node.
|
Sample
input |
Sample
output |
|
6 1 5 3 2 6 3 6 1 1 1 3 5 4 6 4 |
5 9 10 10 8 6 |
SOLUTION
dynamic programming - tree
Algorithm analysis
Let g[i][j]
contains the weight of
the edge between vertices i
and j. Let’s implement the dfs1 function, which for each vertex
v will find the maximum distance depth[v] from v
to a leaf in the subtree rooted at v. If
u1, …, uk
are sons of
v, and depth[ui] is already computed, then
depth[v] = max
(g[v][ui] + depth[ui])
The second depth
first search
dfs2(v, prev, h) for each vertex v will compute the answer res[v]. The second parameter prev
is the ancestor of the vertex
v. Value of h is the maximum possible length from v
to a vertex outside the subtree rooted in v.
First find the largest h1 and second largest h2 distance from v to a leaf in a subtree rooted at v (h1
≥ h2).
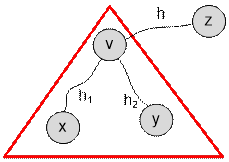
Note that h1 = ![]() , where the maximum is taken over all sons to of the vertex v. Respectively h2 is the second maximum of the indicated sum. Note also that the values of h1 and depth[v] are the same.
, where the maximum is taken over all sons to of the vertex v. Respectively h2 is the second maximum of the indicated sum. Note also that the values of h1 and depth[v] are the same.
The largest possible distance res[v] from v to any vertex
of the tree is
max(h, depth[v])
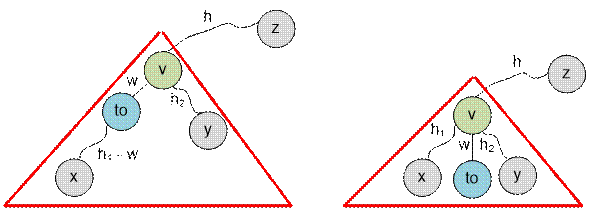
Let to be the
son of the vertex v lying on the path of length
h1 from v
to the farthest leaf
(picture on the left). Then, when
entering to, the longest distance from to to a vertex outside the subtree rooted in to is max(h, h2) + w, where w = g[v][to]. Therefore, a recursive call to
dfs2(to,
v, max(h, h2) + w) will take place.
Let the son to
of the vertex v does not lie on the
longest path h1 (picture on the right). Then, when entering
to, the longest distance from to to a vertex outside the subtree rooted in to will be max(h, h1) + w, we make a recursive call dfs2(to, v, max(h, h1) + w).
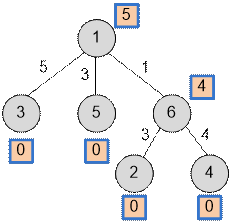
Example
With the first depth first traversal near each vertex v compute the value depth[v].
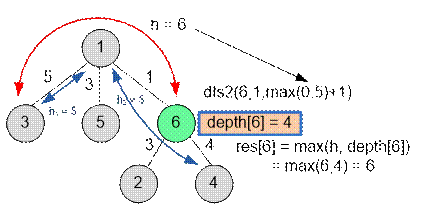
Second depth first search. For the vertex v = 1, the value h =
0, the largest distances to the leaves will be h1 = 5 and h2 = 5. When entering vertex 6,
the depth first search will be called with parameters dfs2(6, 1, max(0, 5) + 1) or dfs2(6, 1, 6), that is, at the vertex 6, the value h = 6. During the first dfs, depth[6] = 4 was computed. Therefore, res[6] = max(h, depth[6]) = max(6, 4) = 6.
Algorithm realization
Store the
weighted tree in the adjacency list g. Declare the arrays.
vector<vector<pair<int,int> > >
g;
vector<int> depth, res;
The maximum
distance from vertex v to a leaf in a
subtree rooted in v is computed in depth[v]
using the dfs1 function.
void dfs1(int v, int prev = -1)
{
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if(to != prev)
{
dfs1(to, v);
depth[v] = max(depth[v], depth[to] + w);
}
}
}
The second depth first search dfs2 for each vertex v finds the
longest possible distance res[v] to any vertex of the tree.
void dfs2(int v, int prev = -1, int h
= 0)
{
res[v] = max(h, depth[v]);
Compute the largest h1 and second largest h2 distance from v to
a leaf in a subtree rooted at v.
int h1 = 0, h2 = 0;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if (to != prev)
{
int h = depth[to] + w;
if (h > h1) h2 = h1, h1 = h; else
if (h > h2) h2 = h;
}
}
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].first;
int w = g[v][i].second;
if (to == prev) continue;
if(h1 == depth[to] + w)
dfs2(to,v,max(h,h2) + w);
else
dfs2(to,v,max(h,h1) + w);
}
}
The main part of
the program. Read the input
tree.
scanf("%d",&n);
g.resize(n+1);
depth.resize(n+1); res.resize(n+1);
for(i = 0; i < n - 1; i++)
{
scanf("%d %d %d",&u,&v,&dist);
g[u].push_back(make_pair(v,dist));
g[v].push_back(make_pair(u,dist));
}
Run two depth first searches.
dfs1(1);
dfs2(1);
Print the answer.
for(i = 1; i <= n; i++)
printf("%d\n",res[i]);